ریاضیات و صنعت خودروسازی

مسائل ریاضی مشکل یا حلال مشکلات؟ مسئله این است!

نوشته دوم: یک مسئله ریاضیات کلاسیک در حل مشکل خودروهای خودران

تصور کنید یک پارکینگ در نزدیکی یک مرکز خرید بزرگ قرار داره، ماشین خودران وارد میشه و یک ربات خرید هم با قابلیت چانه زنی و گرفتن تخفیف جانانه داخل خودرو لم داده، قبل از اعزام، صاحب ربات بهش آموزش داده تا با کسی درگیر نشه و فحش و بد و بیراه نصیب افرادی که در خیابان آشغال میریزن نکنه. ماشین خودران از بین ماشین های زیادی که هر لحظه موقعیت بعضی از آنها عوض میشه باید عبور کنه این وسط یک بچه هم دست مامانش را ول کرده و داره از این ور به اون ور دور خودش میچرخه. یک الگوریتم مکان یابی خیلی سریع برای پیدا کردن جای پارکینگ که هر لحظه داده های زیادی را پردازش میکنه لازمه تا پدر راننده پورشه ای که اون طرفا پارک هست پدر صاب ماشین بدون راننده را در نیاره و مادر بچه هم پدر این ماشین بی پدر (ببخشید بدون سرنشین) را در نیاره.

مدل های ریاضی کمک بزرگی در یافتن الگوریتم هایی برای مسیریابی خودروهای بدون راننده و نیز پیدا کردن جای پارک مناسب در یک پارکینگ بزرگ می کند. مساله ریاضی متناظر یافتن جای پارکینگ مرتبط با مسائل بهینه سازی و الگوریتم مجموع مربعات است که در دانشگاه پرینستون توسط محقق ایرانی امیر علی احمدی استاد دانشگاه پرینستون و گروه تحقیقاتی اش توسعه یافته است. متن این مجله در مورد اینکه چطور یک مساله کلاسیک ریاضی در خودروهای خودران استفاده می شود را بخوانید.

 

نوشته اول: اتومبیل مدرن مجموعه پیچیده ای از سامانه های مکانیکی، شیمیایی، الکتریکی، هیدرولیک و انواع دیگر سامانه های فیزیکی است که همگی ارتباط تنگاتنگی با ریاضیات دارند. بررسی خواص مواد، مقاومت کششی، آستانه ترک خوردگی و … را می توان با آزمایش و خطا تا حدی پیش برد ولی برای جلوگیریی از هدر رفت هزینه های هنگفت برخی آزمایشات، شبیه سازی کامپیوتری گزینه مناسبی است. تحلیل معادلات ارتعاش مربوط به قطعات درگیر و اثر تغییرات مواد اولیه بر ویژگی های ارتعاش، بررسی هدر رفت انرژی گرمایی و موارد دیگر، در مراحل مدل سازی و استخراج قواعد ریاضی حاکم و تجزیه و تحلیل این معادلات با روش های ریاضیات مدرن انجام می شود. در قرن نوزدهم، دانشمندان روش هایی برای مدل سازی ریاضی انرژی بدست آوردند و از طریق این مدل ها توانستند موتورهای به درد بخور بسازند که نهایتا منجر به ماشین های مدرن شد.

نیکولاس اتو (آلمانی، وفات ۱۸۹۱) دانشمندی بود که یک موتور احتراق داخلی طراحی کرد که به اندازه کافی برای خودروهای عملی مناسب بود. امروز، چرخه ترمودینامیکی اتو، مبنای علمی اغلب ماشین های با توان گازی است (منبع).

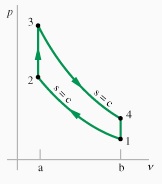بیشترین کارایی موتورهایی که از چرخه اتو استفاده می کنند با فرمول زیر محاسبه می شود:

که در آن  نسبت فشردگی است و   نرخ ظرفیت گرمایی است.

---

گوتلیب دایملر (آلمانی، وفات ۱۹۰۰) ایده چرخه اتو را به خودروهای عملیاتی شامل اولین موتورسیکلت و اولین نسل خودروها تبدیل کرد.

رودلف دیزل (آلمانی، وفات ۱۹۱۳) یک موتور دیزلی ابداع کرد که یک چرخه ترمودینامیکی (و سوخت) متفاوت از چرخه اتو داشت.

لرد کلوین (با نام اولیه ویلیام تامسون) اسکاتلندی وفات ۱۹۰۷ مبنای ریاضی و علمی فیزیک انرژی را بنا نهاد (قوانین ترمودینامیک)

 

مقاله ده صفحه ای زیر را در مورد مدل سازی ریاضی در طراحی صنعتی ببینید: